este es la Imagen del abaco
sábado, 23 de octubre de 2010
Estadística
5.- La estadística es una ciencia referente a la recolección, análisis e interpretación de datos, ya sea para ayudar en la resolución de la toma de decisiones o para explicar condiciones regulares o irregulares de algún fenómeno o estudio aplicado, de ocurrencia en forma aleatoria ocondicional . Sin embargo estadística es mucho más que eso, dado que en otras palabras es el vehículo que permite llevar a cabo el proceso relacionado con la investigación científica También se denominan estadísticas (en plural) a los datos estadísticos
Variable Discreta
4.- Para ordenar los datos de una variable discreta ,que tome pocos valores distintos y estudiarlos más fácilmente, los expresamos en forma de tabla. En una columna se colocan los distintos valores de la variable en orden creciente y la otra el recuento de los datos. El número de veces que se repite un valor se llama frecuencia absoluta se representa por fi.
Podemos representar los datos en tres gráficos, diagrama de barras, polígono de frecuencias y gráfico de sectores.
Diagrama de barras, usado para variables cuantitativas discretas. En el eje OX se señalan los valores de la variable y en el eje OY los valores de la frecuencia absoluta. Se levantan barras de altura igual a la frecuencia absoluta.
Polígono de frecuencias, se obtiene uniendo los extremos superiores de las barras del diagrama.
Gráfico de sectores, es el resultado de dividir un círculo en sectores circulares de ángulos proporcionales a las frecuencias absolutas de cada valor de la variable. Para calcular los grados de cada sector se divide la frecuencia entre el número de datos y se multiplica por 360.Se utiliza para variable discreta y continua
Sistema de Coordenadas
3.- a Un sistema de cordenadas es un conjunto de valores y puntos que permiten definir unívocamente la posición de cualquier punto de un espacio ecuclideo más generalmente variedad diferenciales En fisica se usan normalmente sistemas de coordenadas ortogonales. Un sistema de referencia viene dado por un punto de referencia u origen y una vase octorial otornomas , quedando así definidos los ejes coordenadosdel ángulo central se subtiende un arco del circulo igual al radio del circulo. Tenemos que la longitud la c
ircunferencia está dada por c=2 pi(3.1416) r y que toda la circunferencia subtiene un ángulo de 360º; tenemos entonces que : longitud de la circunferencia en radianes es :
360º = 2 p rad. pi= 3.1416
360º = 2 p rad. pi= 3.1416
Muestra
2.- Las muestras se obtienen con la intención de inferir propiedades de la totalidad de la población, para lo cual deben ser representativas de la misma. Para cumplir esta característica la inclusión de sujetos en la muestra debe seguir una tecnica de muestra . En tales casos, puede obtenerse una información similar a la de un estudio exhaustivo con mayor rapidez y menor coste (véanse las ventajas de la elección de una muestra, más abajo).
Por otra parte, en ocasiones, el muestreo puede ser más exacto que el estudio de toda la población porque el manejo de un menor número de datos provoca también menos errores en su manipulación. En cualquier caso, el conjunto de individuos de la muestra son los sujetos realmente estudiados.
El número de sujetos que componen la muestra suele ser inferior que el de la población, pero suficiente para que la estimación de los parámetros determinados tenga un nivel de confiansa adecuado. Para que el tamaño de la muestra sea idóneo es preciso recurrir a su cálculo.
Por otra parte, en ocasiones, el muestreo puede ser más exacto que el estudio de toda la población porque el manejo de un menor número de datos provoca también menos errores en su manipulación. En cualquier caso, el conjunto de individuos de la muestra son los sujetos realmente estudiados.
El número de sujetos que componen la muestra suele ser inferior que el de la población, pero suficiente para que la estimación de los parámetros determinados tenga un nivel de confiansa adecuado. Para que el tamaño de la muestra sea idóneo es preciso recurrir a su cálculo.
Historia de la Estadística
1.- Los comienzos de la estadística pueden ser hallados en el antiguo Egipto, cuyos faraones lograron recopilar, hacia el año 3050 antes de Cristo, prolijos datos relativos a la población y la riqueza del país. De acuerdo al historiador griego Heródoto, dicho registro de riqueza y población se hizo con el objetivo de preparar la construcción de las pirámides. En el mismo Egipto, Ramsés II hizo un censo de las tierras con el objeto de verificar un nuevo repartoEn el antiguo Israel la Biblia da referencias, en el libro de los Números, de los datos estadísticos obtenidos en dos recuentos de la población hebrea. El rey David por otra parte, ordenó a Joab, general del ejército hacer un censo de Israel con la finalidad de conocer el número de la población
Sistema Sexagesimal
5.- El sistema sexagesimal es un sistema de numeracion poscional que emplea la base sesenta. Tuvo su origen en la antigua babilonia. También fue empleado, en una forma más moderna, por losarabes durante el califato omeya. El sistema sexagesimal se usa para medir tiempos (horas, minutos y segundos) y ángulos (grados, minutos y segundos). En dicho sistema, 60 unidades de un orden forman una unidad.
Ángulos orientados.
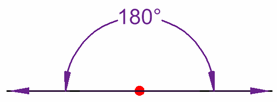
4.- Un ángulo es la porción de plano comprendida entre dos semirrectas que se cortan en un punto denominado vértice a las semirrectas se le llama lados.
Para designar a los ángulos se utilizan tres letras dos para los lados y uno para el vértice que se coloca en medio AOB , o bien con una sola letra colocada en el vértice O, con una letra (normalmente del alfabeto griego) en el interior del ángulo y al lado de un arco de circunferencia que va de un lado a otro, con centro en el vértice a
Para designar a los ángulos se utilizan tres letras dos para los lados y uno para el vértice que se coloca en medio AOB , o bien con una sola letra colocada en el vértice O, con una letra (normalmente del alfabeto griego) en el interior del ángulo y al lado de un arco de circunferencia que va de un lado a otro, con centro en el vértice a
teorema de pitagoras
3.- El terema de pitagoras establece que en un triangulos o rectangulos el cuadrado de la longitud de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de las longitudes de los dos catetos (los dos lados menores del triángulo rectángulo: los que conforman el ángulo recto). Si un triángulo rectángulo tiene catetos de longitudes  y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que:
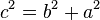
 y
y  , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que: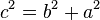
unidad angulares
2.-Comenzamos con la definición de las unidades angulares más conocidas: grados  , minutos (') y segundos ("). Estas unidades son sexagesimales; cada unidad contiene 60 subunidades, por ejemplo: 1 minuto contiene 60 segundos. El sistema establecido en las mediciones de longitud es decimal, 1 metro contiene 10 decímetros, un decímetro 10 centímetros,...
, minutos (') y segundos ("). Estas unidades son sexagesimales; cada unidad contiene 60 subunidades, por ejemplo: 1 minuto contiene 60 segundos. El sistema establecido en las mediciones de longitud es decimal, 1 metro contiene 10 decímetros, un decímetro 10 centímetros,...
El sistema sexagesimal nació en Babilonia, donde se usó en las mediciones astronómicas que, en ese tiempo, consistían en determinar las posiciones de los planetas y estrellas más brillantes con el objeto de establecer un calendario y predecir eclipses, entre otros fines
El sistema sexagesimal nació en Babilonia, donde se usó en las mediciones astronómicas que, en ese tiempo, consistían en determinar las posiciones de los planetas y estrellas más brillantes con el objeto de establecer un calendario y predecir eclipses, entre otros fines
trigonometria Ley de senos.
1.- la ley de los senos es una relacion de tres igualdades que siempre se cumplen entre los lados y angulo de un triangulo cualquiera y que es util para resolver ciertos tipos de problema de triangulos
Donde A, B y C (mayúsculas) son los lados del triángulo, yα,β yγ (minúsculas)
son los ángulos del triángulo:
Observa que las letras minúsculas de los ángulos no están pegadas a su letra mayúscula. O sea, laα está en el ángulo opuesto de A. Laβ está en el ángulo opuesto de B. Y laγ está en el ángulo opuesto de C. Siempre debe ser así cuando resuelvas un triángulo. Si no lo haces así, el resultado seguramente te saldrá mal.
Resolución de triángulos por la ley de los Senos
Resolver un triángulo significa encontrar todos los datos que te faltan, a partir
de los datos que te dan (que generalmente son tres datos).
*Nota: No todos los problemas de resolución de triángulos se pueden resolver con la ley de los senos. A veces, por los datos que te dan, sólo la ley de los cosenos lo puede resolver.
En general, si en un problema de triángulos te dan como datos 2 ángulos y un lado, usa ley de los senos. Si por el contrario te dan dos lados y el ángulo que hacen esos dos lados, usa la ley del coseno.
Supongamos que te ponen el siguiente problema:
Resolver el triángulo siguiente:
Llamemosβ al ángulo de 27° porque está opuesto al lado B;α al ángulo de 43°
y A al lado de 5.
Lo que tenemos entonces es lo siguiente:
A= 5
B=?
C=?
B=?
C=?
α = 43°
β = 27° .
abaco
5.- un abaco es un objeto que sirve para facilitar calculos sencillos como suma, restay multiplicaciones y poeraciones aritmeticas tambien es un cuadro de madera con alambre paralelo por lo que corren bolas movibles y sirve para enseñar el calculo su origen se remota la a la zona asia menor muchos años antes de nuestra era .
desigualdades
4.- Una igualdad es una oración matemática que contiene signo de igual. Por ejemplo:
 no es igual
no es igual
6 + 4 = 10
x + 6 = 10
x + 6 = 10
Una igualdad que tiene variable ( valor desconocido o incógnita) se llama ecuación. Por ejemplo:
x + 6 = 10
Una desigualdad es una oración matemática que contiene un signo de desigualdad. Los signos de desigualdad son:
< menor que
> mayor que
 menor o igual que
menor o igual que
 mayor o igual que
mayor o igual que
Una desigualdad que tiene variable se llama inecuación. Por ejemplo:
x + 3 < 7
(La punta del signo < siempre señala el menor)
Ej. 3 < 4, 4 > 3
¿Cómo resolvemos una inecuación? Para esto tenemos que observar propiedades de las desigualdades. Por ejemplo:
1 < 6
1 + 5 < 6 + 5
1 + 5 < 6 + 5
¿Esto es cierto? Sí. Así que podemos sumar en ambos lados de una desigualdad y sigue cierta.
Otro ejemplo:
2 < 6
2 + -9 < 6 + -9
2 + -9 < 6 + -9
Esto es también cierto. Sigue cierta la desigualdad al sumar en ambos lados un número negativo.
Otro ejemplo con resta:
7 > 4
7 - 3 > 4 – 3
7 - 3 > 4 – 3
La desigualdad sigue siendo cierta al restar un número negativo.
Aquí tenemos otro ejemplo pero esta vez restando un número negativo en ambos lados de la desigualdad:
2 < 82 - (-3) < 8 - (-3) reta un numero es igual que sumar su pouesto . 2 + 3 < 8 + 3 5 < 11 |
La desigualdad es cierta al restar un número negativo de ambos lados.
Multiplicación con números positivos:
3 < 7
3 * 6 < 7 * 6
3 * 6 < 7 * 6
La desigualdad es cierta al multiplicar un números positivos en ambos lados.
Multiplicación con números negativos:
4 > 1 4 · -2 > 1 · -2 -8 > -2 falso |
funciones
3.- el desarrollo de funciones nos lleva a generara una serie de reglas qye permite tomar decisiones acerca de los dominios y codominios entre ortos esta combinacion de operaciones algebraicas de las funciones
productos notables
2.- es el nombre que reciben aquellas multiplocaciones con expreciones algebraicas cuyo resultado puede ser escrito por simple inspeccion sin verificar la multiplicacion que cumplen ciertas reglas figas . su aplicacion simplifica y sistematizar la solucion de muchas multiplicaciones habituales.
potencia
1.- producto que resusulta multiplicar una cantidad o expresion por si misma una o mas veces
angulo complementario
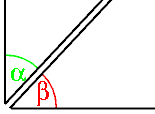
5.- los angulos complementarios son aquellos cuya suma de medidas de90º grados exagesimales si dos angulos complementarios son adyacentes los lados no comunes de los dos forman un angulo recto.
asi para obtener el angulo complementario de a que tiene una amplitud de 70 se restara α de 90°
β = 90° – 70º = 20º el angulo beta es complementaria de alfa)
lunes, 18 de octubre de 2010
HIMNO DE MI COLEGIO JUAN FANCISCO DE LA BODEGA Y QUADRA
HIMNO JUANFRANCISCANO
En Juan Francisco
De la Bodega y Quadra
Tenemos un ejemplo
A seguir
Y es el puerto
Del callao el escenario
Que alberga
Nuestra casa estudiantil
Juan Franciscano
Tuyo es el futuro
Sin en tu quehacer
Pones fuerza y voluntad
Avanza firme
Con paso seguro
Se fiel reflejo
De nuestro mentor
Ahora es el momento
Aquí es el lugar
Que nuestras fortalezas
Debemos demostrar
La ciencia es nuestra arma
Escudo s el saber
Sea nuestra consigna
Vencer, vencer, vencer
En Juan Francisco
De la Bodega y Quadra
Tenemos un ejemplo
A seguir
Y es el puerto
Del callao el escenario
Que alberga
Nuestra casa estudiantil
Juan Franciscano
Tuyo es el futuro
Sin en tu quehacer
Pones fuerza y voluntad
Avanza firme
Con paso seguro
Se fiel reflejo
De nuestro mentor

Suscribirse a:
Comentarios (Atom)